樹莓派溫度
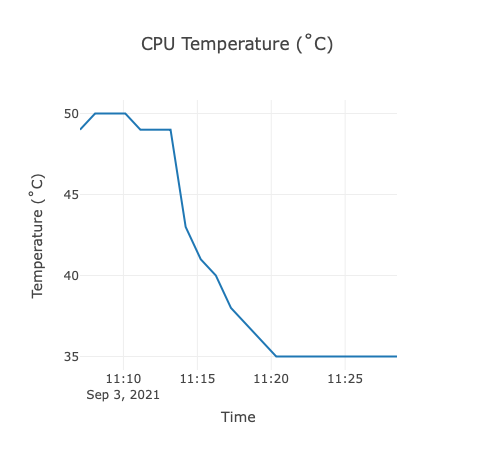
大概是前一陣子,我發現一個叫Anvil的東西,使用起來非常簡單,我拿來監測樹莓派的溫度與CPU使用情況。我把風扇打開,然後出現一條陡峭的下降曲線,我試圖去描述它,這應該不是很困難的事情。
考慮這樣一個模型,一個長方體,不過只關心上下兩個面,間距為$l$,這樣就變成一個一維的問題。這樣的近似是有道理的,因為CPU很薄,而長寬尺寸相對它而言即為無窮大。下底面是CPU的等效溫度$v_0$,上底面是等效環境溫度$v_2$,傳感器在這兩個底面之間的某個位置,暫時不考慮具體在什麼地方。
熱傳導
先做一個變換
$$
v = v_0 + \frac{v_2 - v_0}{l}x + u
$$
這裡以下底面為座標原點,$x$為到下底面的距離。假設導熱係數為$k$,這樣寫出熱傳導方程
$$
u_t - ku_{xx} = 0
$$
以及齊次邊界條件,即$u$在上下底面為零。採用分離變數法,令$u = X(x)T(t)$,得到關於時間的方程
$$
T’ + \lambda kT = 0
$$
以及關於位置的方程
$$
X’’ + \lambda X = 0
$$
這個方程的解為
$$
X = A\sin(\sqrt{\lambda}x) + B\cos(\sqrt{\lambda}x)
$$
由於$X(x=0) = 0$,所以第二個解要捨棄。考慮到$X(x=l) = 0$,解出特徵值$\lambda$為
$$
\lambda = \frac{n^2\pi^2}{l^2}
$$
這樣$u$的解為
$$
u = \sum_{n = 1}^\infty A_n\sin(\frac{n\pi x}{l})e^{-\frac{n^2\pi^2kt}{l^2}}
$$
然後考慮初始條件,假設初始時刻原先內部穩定溫度分佈為$v_0 + \frac{v_1 - v_0}{l}x$,其中$v_1$為打開風扇前/後原先上表面等效溫度,帶入$u$並兩邊同時乘以$\sin(\frac{n\pi x}{l})$並積分,可以求出係數$A_n$
$$
A_n = \frac{2}{l}\int_0^l[\frac{v_1 - v_2}{l}x]\sin(\frac{n\pi x}{l})dx = (-1)^{n + 1}\frac{2(v_1-v_2)}{n\pi}
$$
這樣最終結果為
$$
v = v_0 + \frac{v_2 - v_0}{l}x + \sum_{n = 1}^\infty A_n\sin(\frac{n\pi x}{l})e^{-\frac{n^2\pi^2kt}{l^2}}
$$
分析一個特殊情況,假設傳感器在上下底面的中間$x = l/2$,相應溫度為
$$
v(x=l/2) = \frac{v_0 + v_2}{2} + \frac{2(v_1-v_2)}{\pi}\sum_{n = 1}^\infty\frac{(-1)^{n + 1}\sin(n\pi/2)}{n}e^{-\frac{n^2\pi^2kt}{l^2}}
$$
考慮最後求和項,可以寫成
$$
\sum_{n = 1}^\infty\frac{(-1)^{n + 1}\sin(n\pi/2)}{n}e^{-\frac{n^2\pi^2kt}{l^2}} = \sum_{m = 0}^\infty\frac{(-1)^m}{2m + 1}e^{-\frac{\pi^2k}{l^2}(2m+1)^2t}
$$
這樣結果可以寫成
$$
v(x=l/2) = \frac{v_0 + v_2}{2} + \frac{2(v_1-v_2)}{\pi}\sum_{m = 0}^\infty\frac{(-1)^m}{2m + 1}e^{-\frac{\pi^2k}{l^2}(2m+1)^2t}
$$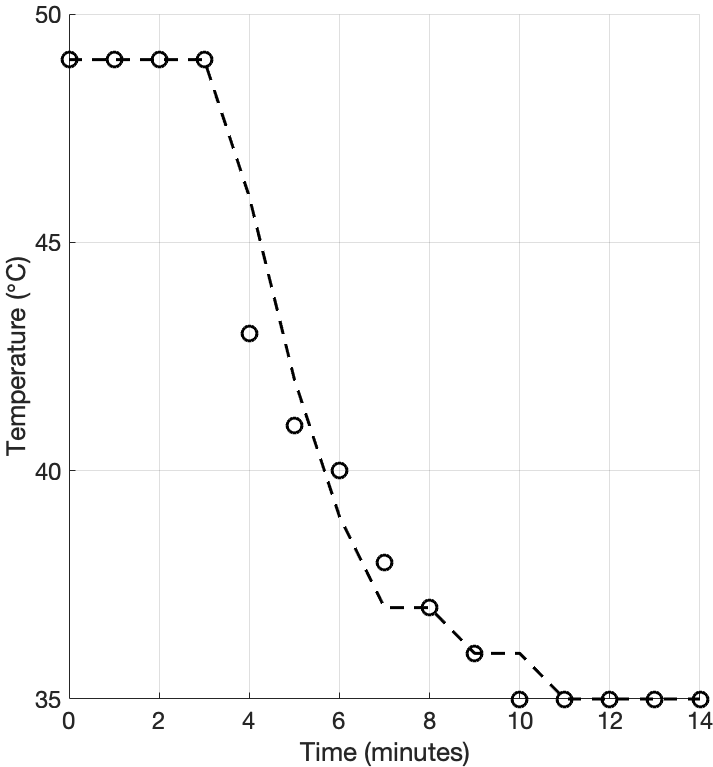
這個結果就是溫度變化曲線。符號為採集數據,虛線為理論結果。由於我在紀錄anvil數據時做了取整處理,因此對相應的理論預測值取整,故局部呈現階梯狀。
脈搏血氧波形
幾天前我的祖父因慢阻肺搶救,當然他現在也沒出來。不過我注意到Pulse Oximeter Pleth的顯示屏上呈現出週期性的簡單的波形,我當時想,我可以解釋它。
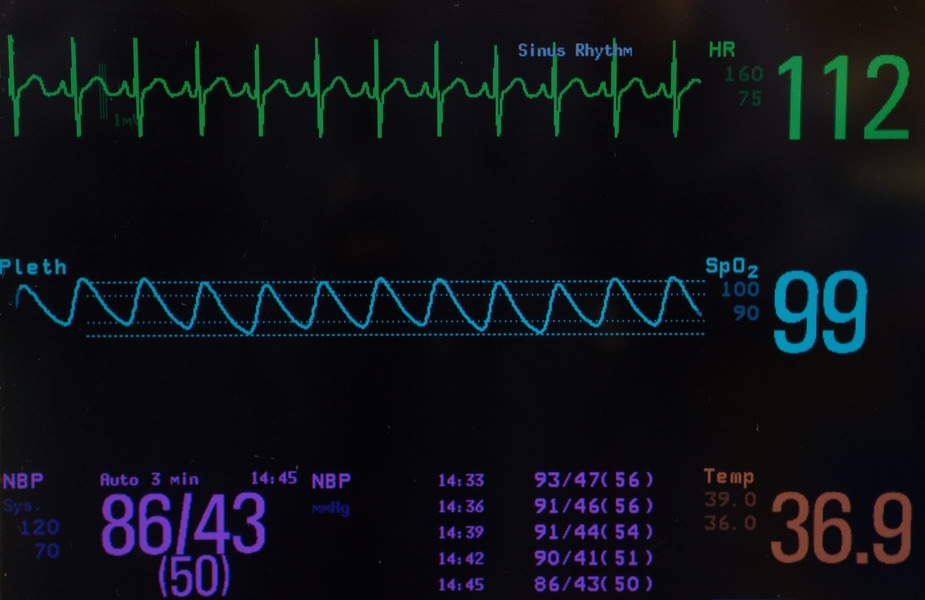
這台儀器實質上測量的是血氧飽和度SpO2,考慮到紅細胞充當氧氣載流子,那麼這個過程等價一個週期性改變初始條件的擴散過程,待測量正比於一段血管中的平均氧氣濃度$\bar c$,那麼考慮如下模型:
一段長度為$l$的血管,其半徑為$r$。富含高濃度$c_0$氧氣的新鮮血液週期性泵進取代原先血管中的血液,同時週遭管壁的氧氣濃度為$c_r$,氧氣可以經由管壁自由擴散至細胞內部,擴散係數為$D$。
擴散
先做一個變換
$$
c = u + c_r
$$
這樣得到相應的擴散方程,在邊界$\rho = r$處$u(\rho=r) = 0$
$$
u_t - D\Delta u = 0
$$
令$u = T(t)R(\rho)$,利用分離變數法,得到關於時間的方程
$$
T’ + k^2DT = 0
$$
以及管徑的亥姆霍茲方程
$$
\Delta R + k^2R = 0
$$
假設管內濃度分佈與與方向無關(各向同性),且與血管前後截面$S$無關(血管無限長)。這裡需要做一些解釋:
第一血管不可能各向同性,一定有些方向吸收能力較強。但這仍不失為一般性假設,即在處理具體問題之前,沒有理由認為哪個方向佔優。
第二血管不可能無限長,但只要週期足夠短,而遠端血液在這麼短的時間內不足以通過擴散方式影響到當前血管,那麼這個假設仍然成立。
這樣就可以得到簡化的,只含有逕向解的亥姆霍茲方程
$$
R’’ + \frac{1}{\rho}R’ + k^2R = 0
$$
如果令$x = k\rho$,以上方程變為
$$
\frac{d^2R}{dx^2} + \frac{1}{x}\frac{dR}{dx} + R = 0
$$
這就是零階的貝索方程,其解為
$$
R = AJ_0(k\rho) + BN_0(k\rho)
$$
考慮在$\rho = 0$時$R$有限,而諾依曼函數$N_0(k\rho)$發散,這樣略去第二個解。假設$x_n^{(0)}$是零階貝索函數$J_0(x)$的第$n$個正根,這樣解出特徵值$k$
$$
k_n = \frac{x_n^{(0)}}{r}
$$
綜合時間得到$u$的解
$$
u = \sum_{n = 1}^\infty A_nJ_0(k_n\rho)e^{-k_n^2Dt}
$$
現在需要確定係數$A_n$,考慮初始條件$u(t = 0) = c_0 - c_r$,其中$c_0$為初始時刻血管中的氧氣濃度。等式兩邊乘以$J_0(k_n\rho)\rho$再積分
$$
(c_0-c_r)\int_0^rJ_0(k_n\rho)\rho d\rho = A_n\int_0^rJ^2_0(k_n\rho)\rho d\rho
$$
這樣解出係數$A_n$
$$
A_n = \frac{2(c_0-c_r)J_1(k_nr)}{k_nr[J_0^2(k_nr)+J_1^2(k_nr)]}
$$
由於實際測量的是平均濃度$\bar c$,對體積$V$積分
$$
\bar c = \frac{\int cdV}{\int dV} = \frac{c_rV + \int udV}{V} = c_r + \sum_n\frac{2}{k_nr}A_nJ_1(k_nr)e^{-k_n^2Dt}
$$
得到的濃度僅為時間的函數。接下來考慮血液泵進過程,假設經過$\Delta t$時間後血液前進速度為$v$,且在此取代過程中忽略新舊血氧在其接觸界面上的擴散以及新血液中的氧氣滲透進血管壁的過程,那麼平均氧氣濃度$\bar c’$近似為
$$
\bar c’ \approx \frac{Sv(t-\Delta t)c_0 + S[l-v(t-\Delta t)]\bar c_t}{V} = \frac{v(t-\Delta t)}{l}(c_0-\bar c_t) + \bar c_t
$$
其中$0 < t \leq \frac{l}{v} - \Delta t$,對$t > \frac{l}{v} - \Delta t$的時,則退回到最初$\bar c$的情況。結果中可以不出現推進速度以及血管長度,令$\Delta t’ = l/v$表示取代過程所用時間,這樣一個週期的長度為$\Delta t + \Delta t’$。考慮在$k(\Delta t+\Delta t’) \leq t < (k+1)(\Delta t+\Delta t’)$一個週期內,由擴散而消耗的平均氧氣濃度可以寫成
$$
\bar c = c_r + \sum_n\frac{2}{k_nr}A_nJ_1(k_nr)e^{-k_n^2D[t-k(\Delta t+\Delta t’)]}
$$
接下來考慮在一個週期的前半段$k(\Delta t+\Delta t’) \leq t < (k+1)\Delta t + k\Delta t’$時間內,血液中的氧氣濃度即為$\bar c$,而在一個週期的後半段$(k+1)\Delta t + k\Delta t’ \leq t < (k+1)(\Delta t+\Delta t’)$時間內,血液中的氧氣濃度為$\bar c’$
$$
\bar c’ = \frac{t - (k+1)\Delta t - k\Delta t’}{\Delta t’}(c_0-\bar c_t) + \bar c_t
$$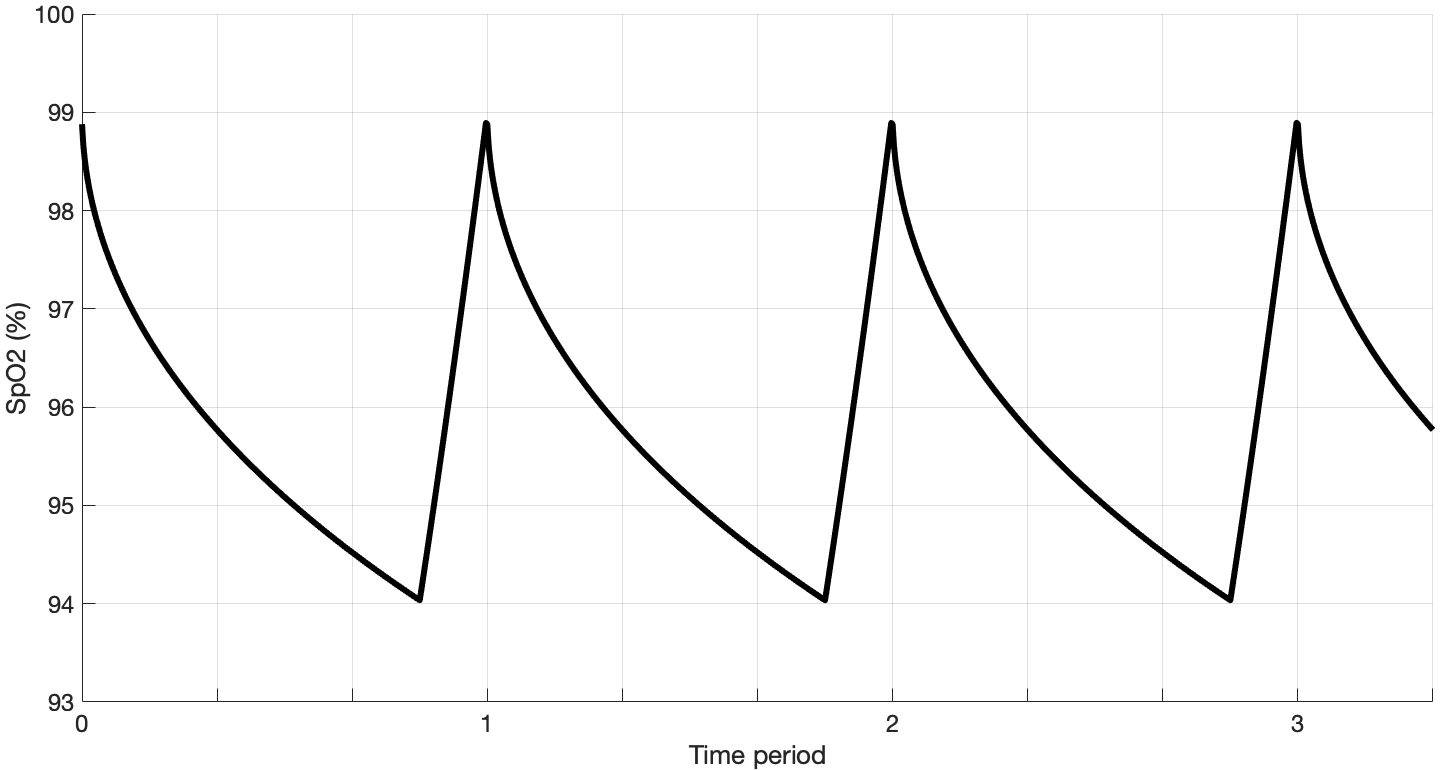
把理論結果畫出來便是這樣。注意到在最大/小值附近並不平滑,這是由於在取代過程中的擴散效應不能忽略,而我只做了簡單的近似處理。描述它需要更高階的修正,在我看來已經沒有什麼太大必要。
後記
熱傳導與擴散都屬於輸運方程,即拋物型偏微分方程。通過分離變數都可以得到一個空間的亥姆霍茲方程與時間的一階常微分方程,而前者的差異僅取決於邊界條件。
以上便是過去一週我在生活中觀察到並試圖解釋的兩個現象,因為它們從屬於同一類方程,所以整理在此。