引言
利用簡單方法推導懸鏈線方程。
推導
模型
考慮不可伸長的懸索兩端固結於座標分別為$A(x_1,y_1)$和$B(x_2,y_2)$,密度為$\rho$,長度為$L$,求解其形狀。
變分
直接考慮變分。
考慮繩索的長度為$s$,將一小段繩索的長度記為$ds$,那麼它相對參考平面的重力勢能應該為
$$
dV = \Delta mgh = \rho gyds + V_0
$$
那麼總勢能為
$$
V = \int_A^B\rho gyds + V_0
$$
$V_0$是參考平面的勢能,它只貢獻一個常數,對形狀沒有影響。作一個變換消去裡面的係數,可以使問題簡化。令$\tilde V = \frac{V - V_0}{\rho g}$
$$
\tilde V = \int_A^Byds
$$
要求勢能最低,也就是對$\tilde V$的等$x$變分為零。換言之,能量與位置$x$無關,而與形狀$y$有關。
$$
\delta\tilde V = \delta\int_A^Byds = 0
$$
我們知道
$$
ds = \sqrt{dx^2 + dy^2}
$$
$ds$包括了$dy$,因此變分要取到$ds$上。同時變分與微分符號可以交換,即
$$
\delta(ds) = \frac{dy\delta(dy)}{ds} = \frac{dy}{ds}d(\delta y)
$$
因此
$$
\begin{aligned}
\delta\int_A^Byds =& \int_A^B\left[\delta yds+y\delta(ds)\right]\\
=& \int_A^B\left[\delta yds+y\frac{dy}{ds}d(\delta y)\right]\\
=& \int_A^B\left[\delta yds-d(y\frac{dy}{ds})\delta y\right] + \left[y\frac{dy}{ds}\delta y\right]_A^B
\end{aligned}
$$
最後一步用到分部積分,考慮端點是固定的,$\delta y(A) = \delta y(B) = 0$,因此
$$
\delta\int_A^Byds = \int_A^B\left[1-\frac{d(y\frac{dy}{ds})}{ds}\right]\delta yds = 0
$$
由於$\delta y$是任意的,如果要上式恆等於零,則必有
$$
1-\frac{d(y\frac{dy}{ds})}{ds} = 0
$$
這就是懸鏈線的方程。
求解
它的形式可能跟常見的結果不太一樣,但沒有關係,是同一個東西。這是一個很容易求解的方程,
$$
d(y\frac{dy}{ds}) = ds
$$
兩邊同時積分,則有
$$
y\frac{dy}{ds} = s + c_1
$$
$c_1$是積分常數,與後面的$c_2$及$c_3$相同。再積分一次,則有
$$
y^2 = s^2 + 2c_1s + c_2
$$
這個過程是非常簡單的。
簡化
考慮到常見的懸鏈線方程並不含有$s$,而是寫成關於位置的函數。只需稍作變形即可,由上述結果解出$s$
$$
s = -c_1 \pm \sqrt{c_1^2 - c_2 + y^2}
$$
為何有正負?你畫一下圖就知道,同一個高度可以對應兩個長度。同時已經知道
$$
\frac{ds}{dy} = \frac{\sqrt{dx^2 + dy^2}}{dy} = \sqrt{1 + (\frac{dx}{dy})^2}
$$
我們將已經求出的結果對$y$取一次微分
$$
\frac{ds}{dy} = \pm\frac{y}{\sqrt{c_1^2 - c_2 + y^2}}
$$
比較上面兩式,不難得到
$$
1 + (\frac{dx}{dy})^2 = \frac{y^2}{c_1^2 - c_2 + y^2}
$$
化簡得到
$$
\frac{dx}{\sqrt{c_2 - c_1^2}} = \frac{dy}{\sqrt{c_1^2 - c_2 + y^2}}
$$
令$a = \sqrt{c_2 - c_1^2}$,考慮積分換元$y = a\tilde y$,則
$$
\frac{dx}{a} = \frac{d\tilde y}{\sqrt{\tilde y^2 - 1}}
$$
兩邊積分,得到
$$
\frac{x}{a} + c_3= \text{acosh}(\tilde y)
$$
也就是
$$
\tilde y = \cosh\left[\frac{x}{a} + c_3\right]
$$
這就是常見的雙曲餘弦結果。
參數
若要確定一條懸鏈線,除了固定首尾兩端外,還需要明確繩索長度。如果這三個條件都唯一確定,可以想見將僅有一條懸鏈線與之對應。首尾端點座標,加上繩索總長,可以確定三個未知參數。將解出的結果重寫一遍,繩索長度與高度的關係有
$$
y^2 = s^2 + 2c_1s + c_2
$$
繩索的形狀則為
$$
\frac{y}{a} = \cosh\left[\frac{x}{a} + c_3\right]
$$
其中$a = \sqrt{c_2 - c_1^2}$。然而此處需要注意,我有明確$y$是什麼嗎,並沒有,我只說它是相對某個參考平面的高度,是哪個平面根本無所謂。但第二個方程卻暗含了$y \ge a$的條件,這顯然是有問題的。
這也是所有常見推導都不曾提過的事情,考慮相對高度,繩索方程應該寫成這樣子
$$
\frac{y - y_0}{a} = \cosh\left[\frac{x}{a} + c_3\right]
$$
其中$y_0$是參考平面的高度,現在的$y$才可以任意取值。這才是正確的形式,三個獨立的參數,正好對應三個限制條件。同理長度的方程應該為
$$
(y-y_0)^2 = (s+c_1)^2 + a^2
$$
一樣有三個未知參數,需要三個限制條件求解。
這樣當然可以解出來,但現實生活中兩端一般是等高的,為了方便起見,假設$A(-D/2,H)$與$B(D/2,H)$在選取的座標原點兩側,這樣有
$$
\begin{aligned}
& \frac{H - y_0}{a} = \cosh\left[-\frac{D}{2a} + c_3\right]\\
& \frac{H - y_0}{a} = \cosh\left[\frac{D}{2a} + c_3\right]\\
& (H-y_0)^2 = c_1^2 + a^2\\
& (H-y_0)^2 = (L+c_1)^2 + a^2
\end{aligned}
$$
三個條件卻有四個方程,這是因為繩索在起點為零,在終點等於全長$L$。四個方程解出上述四個未知量
$$
\begin{aligned}
& c_3 = 0\\
& c_1 = -\frac{L}{2}\\
& a\cdot\sinh(\frac{D}{2a}) = \frac{L}{2}\\
& y_0 = H - a\cdot\cosh(\frac{D}{2a})
\end{aligned}
$$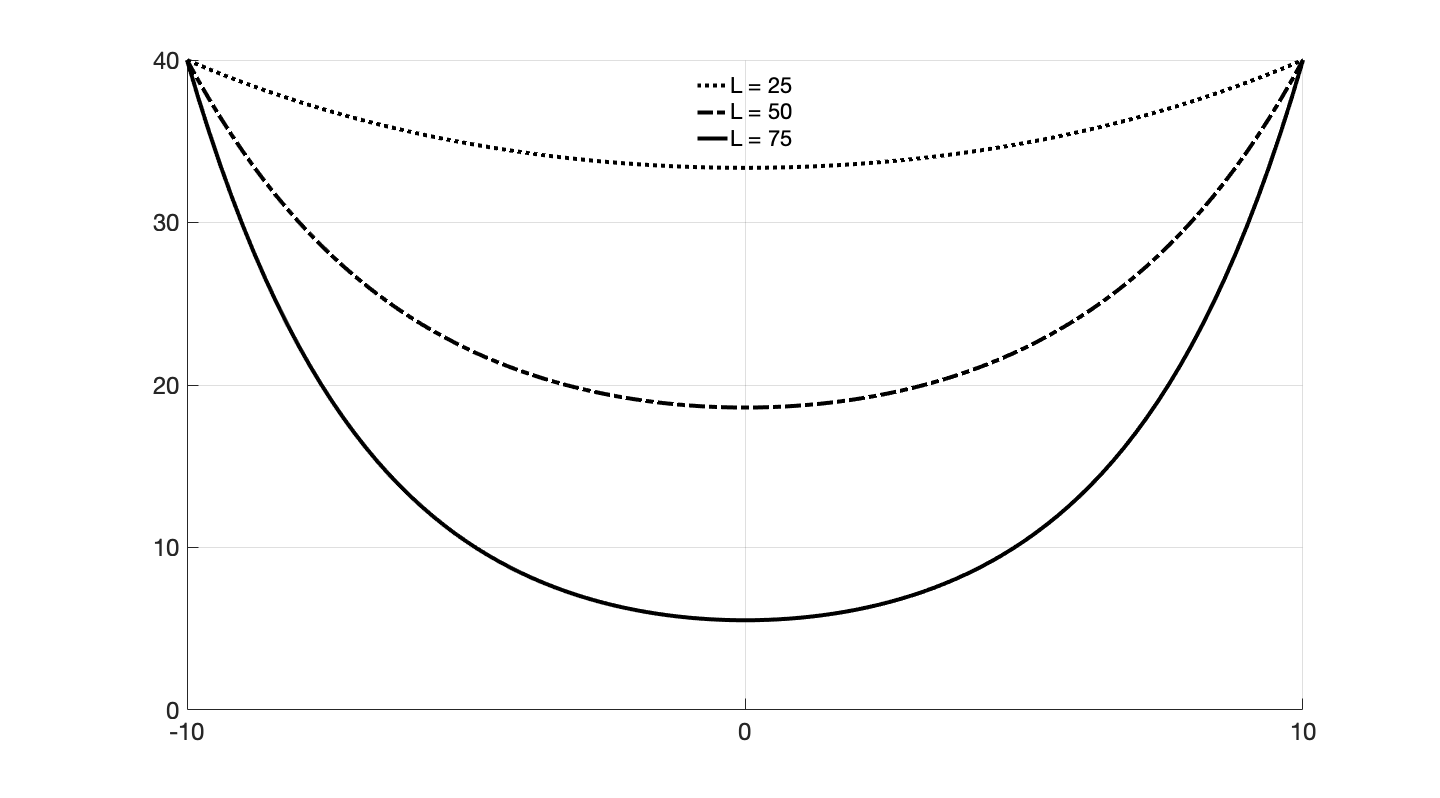
其中$a$不能直接解出,需要數值方法。
一般情況
接續上面的問題,考慮不等高的情況,這時候結果要複雜一些,首先還是一樣聯立方程
$$
\begin{aligned}
& \frac{y_1 - y_0}{a} = \cosh\left[\frac{x_1}{a} + c_3\right]\\
& \frac{y_2 - y_0}{a} = \cosh\left[\frac{x_2}{a} + c_3\right]\\
& (y_1-y_0)^2 = c_1^2 + a^2\\
& (y_2-y_0)^2 = (L+c_1)^2 + a^2
\end{aligned}
$$
其中$a$由這個方程解出
$$
a = \frac{\sqrt{L^2 - (y_2-y_1)^2}}{2\sinh(\frac{x_2 - x_1}{2a})}
$$
在求出$a$後,可以解出$c_3$
$$
c_3 = \text{atanh}\left[\frac{y_2 - y_1}{L}\right] - \frac{x_1 + x_2}{2a}
$$
已知$a$和$c_3$的情況下可以求出$c_1$
$$
c_1 = a\cdot\sinh(\frac{x_1}{a}+c_3)
$$
最後可以得到$y_0$
$$
y_0 = y_1 - a\cdot\cosh(\frac{x_1}{a} + c_3)
$$
只是略為麻煩一些。因此確定端點位置,以及繩索長度,就可以得到唯一曲線。
長度測量
實際上,知道$a$就可以測出全長$L$
$$
L = \sqrt{(y_2-y_1)^2 + 4a^2\sinh^2(\frac{x_2 - x_1}{2a})}
$$
對懸索橋來說,塔架是等高的,因此還可以簡化為
$$
L = 2a\sinh(\frac{x_2 - x_1}{2a})
$$
因此知道$a$和跨度$x_2-x_1$即可知道懸索的長度。對$a$的測量可以考慮對曲線底部作近似,試將座標原點移到弧線的最低點,那麼此時方程為
$$
y = a\left[\cosh(\frac{x}{a})-1\right]
$$
在底部作展開
$$
y = a\left[\cosh(\frac{x}{a})-1\right] \approx \frac{x^2}{2a}
$$
因此只考慮在最低點附近的曲線完全是可以用拋物線作近似的。可以測出相對最低點附近的一點的橫向距離為$\Delta x$,上升距離為$\Delta y$
$$
a = \frac{\Delta x^2}{2\Delta y}
$$
由拋物線方程解得係數,代回可以求出總長度。
對於鄰近但不包含曲線最低點的區域,可以考慮斜率
$$
y’ \approx \frac{x}{a}
$$
注意到斜率將均勻變化,因此可以任意固定一起始點,鄰近一點相對起始點的橫向距離為$\Delta x_1$,上升距離為$\Delta y_1$。接下來沿著該方向尋找第三點,且該點相對第二點的橫向距離為$\Delta x_2$,上升距離為$\Delta y_2$
$$
a = \frac{\Delta x_1\Delta x_2}{2}\cdot\frac{\Delta x_1 + \Delta x_2}{\Delta y_2\Delta x_1 - \Delta y_1\Delta x_2}
$$
特別當$\Delta x_1 = \Delta x_2 = \Delta x$時,實際測量中可以簡化
$$
a = \frac{\Delta x^2}{\Delta y_2 - \Delta y_1}
$$
同樣解得係數,代回即可以求出總長度。
後記
整個過程是非常簡單的,沒有稍微複雜一點的計算。