引言
這篇是對此前一篇的擴展,引入具體實例加以計算。
懸索
懸索橋的重量完全壓在懸索上,因此在考慮時可以近似略去橋身而將總質量分攤在懸索上,這也是其呈現懸鏈狀的原因。但它不是真正的懸鏈線,確切講是分段的,只有垂直吊著橋身的線足夠密集,才得到真正的懸鏈線。不過這無關緊要,現實中當成懸鏈線處理是完全可以接受的。
懸索長度
由此前一篇可以知道,要計算懸索長度,則
$$
L = \sqrt{(y_2-y_1)^2 + 4a^2\sinh^2(\frac{x_2 - x_1}{2a})}
$$
其中懸鏈係數$a$可以用拋物線估計,即測出相對最低點附近的一點的橫向距離為$\Delta x$,上升距離為$\Delta y$
$$
a = \frac{\Delta x^2}{2\Delta y}
$$
抑或是考慮斜率的變化,即任意固定一起始點,鄰近一點相對起始點的橫向距離為$\Delta x_1$,上升距離為$\Delta y_1$。接下來沿著該方向尋找第三點,且該點相對第二點的橫向距離為$\Delta x_2$,上升距離為$\Delta y_2$
$$
a = \frac{\Delta x_1\Delta x_2}{2}\cdot\frac{\Delta x_1 + \Delta x_2}{\Delta y_2\Delta x_1 - \Delta y_1\Delta x_2}
$$
考慮現實中的一個例子,金門大橋
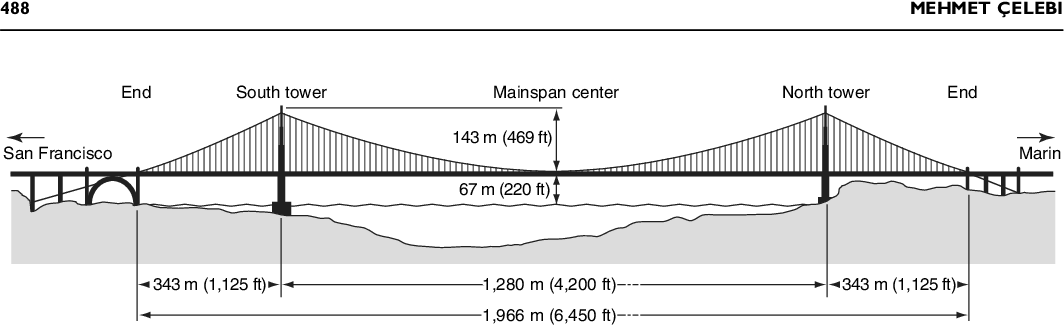
可以分別令$L = 1280$ m,$L_0 = 343$ m,$H = 143$ m。左右兩側的橋下部分懸索的水平與豎直伸長記為
| To Sanfrancisco | To Marin |
|---|---|
| $\Delta x_1 = 248$ m | $\Delta x_2 = 119$ m |
| $\Delta y_1 = 66$ m | $\Delta y_2 = 43$ m |
這個表格中的數據是估計值,由此可以計算出懸索的總長度約為$2450$ m,而眾所週知,金門大橋懸索的真實長度為$2332$ m,相對誤差只有百分之五,這還是在使用非常粗糙近似的情況下。這是因為兩側橋面下方的懸索是直線而非懸鏈線。
後記
據此模型可以推估中間弧段的長度$l_0 = 1323$ m。
又及:我在舊金山機場被偷了兩千五百美元,身無分文地去了達拉斯,這真是一種永生難忘的體驗。