引言
我在看希臘歷史的時候注意到阿基米德曾經證明拋物線下弓形面積是其內接三角形的三分之四倍。
這句話引起了我的興趣,古希臘人代數並不發達,這個證明需要用到微積分,我在猜想他是怎麼得到這個結論的。
我想此處的三角形應該要作個限定,是指弓內最大面積的三角形,否則沒有意義。另外,三角形的另外兩邊又割出了兩個新的弓,從而又可以重複以上操作。那麼從最原始的三角形出發,生出兩個次級三角形,次級三角形又生出新的次級三角形…這樣重複下去,把這些所有的三角形加起來,就是最初三角形底邊割出的弓的面積。
那麼轉化後的問題是這樣,如果兩個次級三角形的面積和該三角形的比值為一個定值,不難算出這種情況下應該為四分之一,那麼最後弓的面積將是一個幾何級數。由簡單的代數知識,原命題等價於證明兩個次級三角形的面積和是該三角形面積的四分之一。
證明
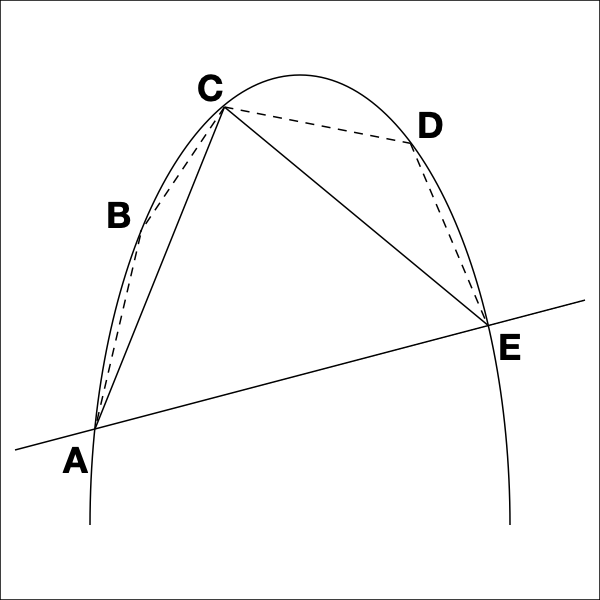
假設拋物線方程為$y = ax^2,\ a < 0$,A到E點的坐標分別為$(x_n,y_n),\ n=1,2,3,4,5$。三角形ACE的面積記作$s_1$,由該三角形兩條邊生成的兩個次級三角形ABC和三角形CDE的面積分別記作$s_2$與$s_3$。
由拋物線的性質,C點要保證三角形ACE的面積最大,則要求C盡可能遠離直線AE,你可以用無數條與之平行的直線去割拋物線,最終會得到只有一個交點的情況,該點即為切點,也就是C的位置。拋物線的切線斜率是簡單的一次函數,希臘人早已知道這點。
因此
$$
x_3 = \frac{1}{2a}\frac{y_5 - y_1}{x_5 - x_1} = \frac{1}{2a}\frac{a(x_5^2-x_1^2)}{x_5 - x_1} = \frac{x_1 + x_5}{2}
$$
該切點的橫坐標即為端點的算數平均,這也是拋物線的性質。現在計算$s_1$
$$
2\vec s_1 = \vec{CA}\times\vec{CE} =
\left|
\begin{matrix}
\mathbf{i} & \mathbf{j} & \mathbf{k}\\
x_1 - x_3 & y_1 - y_3 & 0\\
x_5 - x_5 & y_5 - y_5 & 0
\end{matrix}
\right|
= \mathbf{k}
\left|
\begin{matrix}
x_1 - x_3 & y_1 - y_3\\
x_5 - x_5 & y_5 - y_3
\end{matrix}
\right|
$$
注意到
$$
\begin{aligned}
& x_1 - x_3 = x_1 - \frac{x_1 + x_5}{2} = \frac{x_1 - x_5}{2}\\
& x_5 - x_3 = x_5 - \frac{x_1 + x_5}{2} = \frac{x_5 - x_1}{2}
\end{aligned}
$$
以及
$$
\begin{aligned}
& y_1 - y_3 = ax_1^2 - ax_3^2 = a(x_1+x_3)(x_1-x_3)\\
& y_5 - y_3 = ax_5^2 - ax_3^2 = a(x_5+x_3)(x_5-x_3)
\end{aligned}
$$
因此
$$
2\vec s_1 = \mathbf{k}\cdot a(x_1-x_3)(x_5-x_3)(x_5-x_1) = -\frac{a}{4}\mathbf{k}(x_5-x_1)^3
$$
類似可以得到$2\vec s_2 = \vec{BA} \times \vec {BC} = -\frac{a}{4}\mathbf{k}(x_3-x_1)^3$以及$2\vec s_3 = \vec{DC} \times \vec {DE} = -\frac{a}{4}\mathbf{k}(x_5-x_3)^3$。看看加起來是什麼,考慮到
$$
A^3 + B^3 = (A+B)(A^2-AB+B^2) = (A+B)[(A+B)^2-3AB]
$$
這裡$A = x_3 - x_1 = \frac{x_5 - x_1}{2}$,$B = x_5 - x_3 = \frac{x_5 - x_1}{2}$,因此$A + B = x_5 - x_1$,$AB = \frac{(x_5-x_1)^2}{4}$
$$
(x_3-x_1)^3 + (x_5-x_1)^3 = (x_5-x_1)[(x_5-x_1)^2-\frac{3}{4}(x_5-x_1)^2] = \frac{1}{4}(x_5-x_1)^3
$$
因此
$$
\vec s_2 + \vec s_3 = \frac{1}{4}\vec s_1
$$
這個比值確實是最初猜想的四分之一,如果把直線AE割下的弓形面積記為$s$,因此有
$$
s = s_1[1 + \frac{1}{4} + \frac{1}{4^2} + … + \frac{1}{4^{n - 1}}] = \frac{4}{3}[1-\frac{1}{4^n}]s_1 \approx \frac{4}{3}s_1
$$
這就是阿基米德的結論。
後記
早期我在讀自然哲學的數學原理的時候,有過類似的困惑:我不太看得懂牛頓寫了什麼,但我大概能猜出他做的事情,應該是和阿基米德類似的方法。阿基米德是希臘化時代的人,彼時希臘文明也走向它的終點了。這是一段頗令人感傷的現實,你可以理解為十七世紀的歐洲重新撿起了兩千年前希臘人的東西,並重新塑造了現代數學的基礎。演繹、實證和邏輯,這些都只曾出現於希臘文明之中:是那些希臘人,他們最早進行文學批評,最早丈量了地球,最早思考世界的本原以及組織民主社會的方式。因此從某種意義上說,現代科學,以至於現代文明,只可能在希臘文明中產生,而足以睥睨後世拙劣而平庸的仿效者。