引言
我住在Dallas的時候,因為鄰近Lovefield機場,幾乎時時都有飛機從頭頂掠過。香港的機場遠離市區,故飛機雖多,但都因其在高空的緣故,看起來就沒有視覺上的震撼。這也讓我萌生出估算其距離的想法,我思考了一下,認為是可行的,只需要測量兩個角度即可。
模型
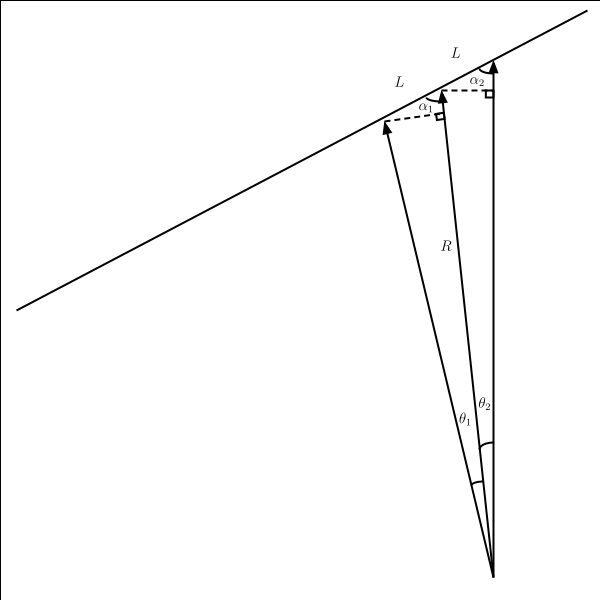
考慮飛機從自左下方飛掠觀測點,$L$表示機身的長度。$R$表示飛機到觀測點的距離,而$\theta_1$和$\theta_2$分別為兩次觀測的角度。
估計值
用直角邊來代替弧長,這對小角度是成立的
$$
R \approx \frac{L\sin\alpha_1}{\theta_1} \approx \frac{L\sin\alpha_2}{\theta_2}
$$
此外由幾何關係有
$$
\alpha_1 = \alpha_2 + \theta_2
$$
由這兩個條件可以解出$\alpha_2$
$$
\frac{\theta_1}{\theta_2} \approx \frac{\sin\alpha_1}{\sin\alpha_2} = \cos\theta_2 + \frac{\sin\theta_2}{\tan\alpha_2} \approx 1 + \frac{\theta_2}{\tan\alpha_2}
$$
這裡考慮到了$\theta_1$與$\theta_2$都是小角度的條件,進而可以得到距離
$$
R \approx \frac{L\sin\alpha_2}{\theta_2} = \frac{L}{\sqrt{\theta_2^2 + (\theta_1/\theta_2-1)^2}}
$$
後記
雖然飛機的長度並不一致,但都約莫在五十米左右,並不會帶來量級上的誤差。困難在於對小角度的估計。關於這一點沒有什麼好辦法。
我想我會懷戀這裡,懷戀德州,懷戀那些站在天橋伸直手臂、乜斜右眼用拇指測量天空日子。因為那裡有自由的空氣,虔誠的信徒,還有最珍貴的朋友。