引言
我最初想到這個問題時,是我在南京南站看到巨幅廣告牌。它的內容我現在已經完全忘記,只留下一個logo的印象:一個十點十分三十秒的時鐘,指針排成丫字形狀。
我不知道它是什麼意思,我猜它或許是想把錶盤三等分,但顯然那種分法是錯的。我沒有理由相信十點和十點十分的時針會指在同一個位置上。接著我問自己,是否存在這樣的一個時刻,指針將錶盤三等分?我認為這樣的時刻是不存在的,可以通過編程發現這一點,但我不知道怎麼證明它。
這是大學時的事了,我昨天突然想起這個陳年舊事來。
模型
這個問題可以簡化為,$N$個不同角速度的點在圓周上運動,考慮其排列問題。默認$\omega_1 \geq \omega_2 \geq … \geq \omega_N$,考慮複數
$$
A = \sum_n e^{i(\omega_nt + \phi_n)}
$$
那麼等分問題等價於求解
$$
|A|^2 = 0
$$
如果要它們排列成一個直線,則等價於求解
$$
|A|^2 = N^2
$$
下面略去相位$\phi_n$考慮提到的具體的例子。
證明
這裡將秒鐘,分針,時針的速度分別記作$\omega_1 = \frac{2\pi}{60} \text{rad/s}$,$\omega_2 = \frac{2\pi}{3600} \text{rad/s}$,$\omega_3 = \frac{2\pi}{43200} \text{rad/s}$。計算模方
$$
|A|^2 = A\bar A = \sum_{m,n} e^{i(\omega_m-\omega_n)t} = N + 2\sum_{m<n}\cos[(\omega_m-\omega_n)t]
$$
這個方程是沒有零解的。可以簡單證明:不妨假設存在零解,令
$$
J = \cos\alpha + \cos\beta + \cos(\alpha-\beta)
$$
其中$\alpha = (\omega_1 - \omega_2)t$,$\beta= (\omega_1 - \omega_3)t$。則$|A|^2 = 0$等價於求解$J = -3/2$,可以將其改寫為
$$
J = 2\left(\cos\frac{\alpha - \beta}{2} + \frac{1}{2}\cos\frac{\alpha + \beta}{2}\right)^2 -\frac{1}{2}\cos^2\frac{\alpha + \beta}{2} - 1
$$
因此當且僅當$\cos\frac{\alpha - \beta}{2} = -\frac{1}{2}\cos\frac{\alpha + \beta}{2}$且$\cos^2\frac{\alpha + \beta}{2} = 1$時才能滿足條件。由第二個條件可知
$$
\alpha + \beta = 2k\pi
$$
帶入第一個條件,得到
$$
\cos\alpha + \cos\beta = -1
$$
這意味著$\cos\alpha = \cos\beta = -1/2$,但兩角相異。注意$\alpha < \beta$,且$0 \leq \beta - \alpha \leq 22\pi$。下面分兩種情況討論:
- $\alpha = \frac{2\pi}{3} + 2k_1\pi$,$\beta= \frac{4\pi}{3} + 2k_2\pi$,$k_2 \geq k_1$時
- $\alpha = \frac{4\pi}{3} + 2k_1\pi$,$\beta= \frac{2\pi}{3} + 2k_2\pi$,$k_2 > k_1$時
異角
情況一要求$0 \leq k_1 \leq k_2 < 719$,以及比值滿足
$$
\frac{3k_1 + 1}{3k_2 + 2} = \frac{708}{719}
$$
只有$k_2 = 239$唯一解,然而$k_1$解出不是一個整數。
最後情況二要求$0 \leq k_1 < k_2 < 719$,寫出比值
$$
\frac{3k_1 + 2}{3k_2 + 1} = \frac{708}{719}
$$
同理只有$k_2 = 479$唯一解,然而$k_1$解出依然不是一個整數。
綜上所述,零解存在的假設是錯誤的,因此錶盤上不存在將其等分的時刻。至於滿足何種條件才能存在這樣的時刻,參考上述證明過程即可。
討論
既然這樣的時刻不存在,很自然的想法是最接近等分的時刻出現在一天中的什麼時候。一般而言,可以通過計算其導數找到極值點的位置
$$
\frac{d|A|^2}{dt} = -2\sum_{m<n}(\omega_m-\omega_n)\sin[(\omega_m-\omega_n)t] = 0
$$
即求解
$$
\alpha\sin\alpha + \beta\sin\beta + (\beta-\alpha)\sin(\beta-\alpha) = 0
$$
再取一階導數
$$
\frac{d^2|A|^2}{dt^2} = -2\sum_{m<n}(\omega_m-\omega_n)^2\cos[(\omega_m-\omega_n)t]
$$
即極小值滿足要求
$$
\alpha^2\cos\alpha + \beta^2\cos\beta + (\beta-\alpha)^2\cos(\beta-\alpha) < 0
$$
問題在於超越方程難於求解,而且圖像也伴隨著劇烈波動,可以找到很多極小值,但大多不是你需要的。
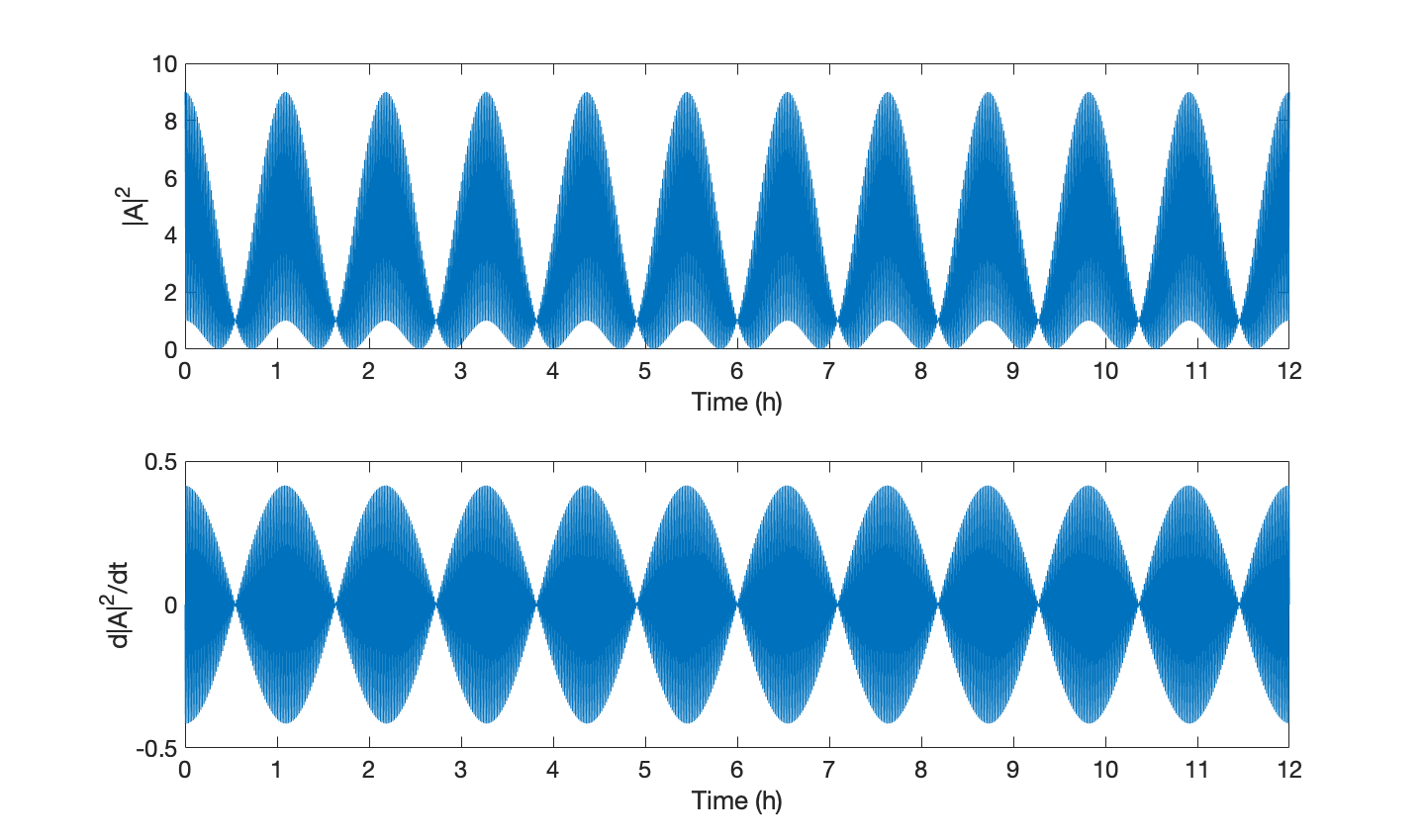
實際上可以換一種思路,根據上節的討論,已經知道
$$
|A|^2 = N + 2J
$$
有理由相信即便零解的兩個條件難以達成,接近零解的點也應在其附近。假定$\cos^2\frac{\alpha + \beta}{2} = 1$仍舊滿足,但$\cos\frac{\alpha - \beta}{2} + \frac{1}{2}\cos\frac{\alpha + \beta}{2} = \epsilon$將等於一個小量,再加上$\alpha / \beta = c$這個條件,很容易解出
$$
\epsilon = (-1)^k\left(\frac{1}{2} + \cos\frac{2k\pi}{1+c} \right)
$$
因此
$$
|A|^2 = 4\epsilon^2 = 4\left(\frac{1}{2} + \cos\frac{2k\pi}{1+c} \right)^2
$$
其中$k$是通過$\alpha + \beta = 2k\pi$定義的,因此其範圍在$0 \leq k \leq 1427$。用$\lfloor x \rfloor$表示不大於$x$的最大整數,則
$$
\cos\frac{2k\pi}{1+c} = \cos\left[2\pi\left(\frac{k}{1+c} - \lfloor\frac{k}{1+c}\rfloor\right)\right]
$$
即等價於尋找小數部分$y = \frac{k}{1+c} - \lfloor\frac{k}{1+c}\rfloor$何時最接近1/3或2/3,然后反求出时间
$$
t = \frac{2k\pi}{2\omega_1-\omega_2-\omega_3}
$$
因為存在22個交點,對應22個最小值的位置。
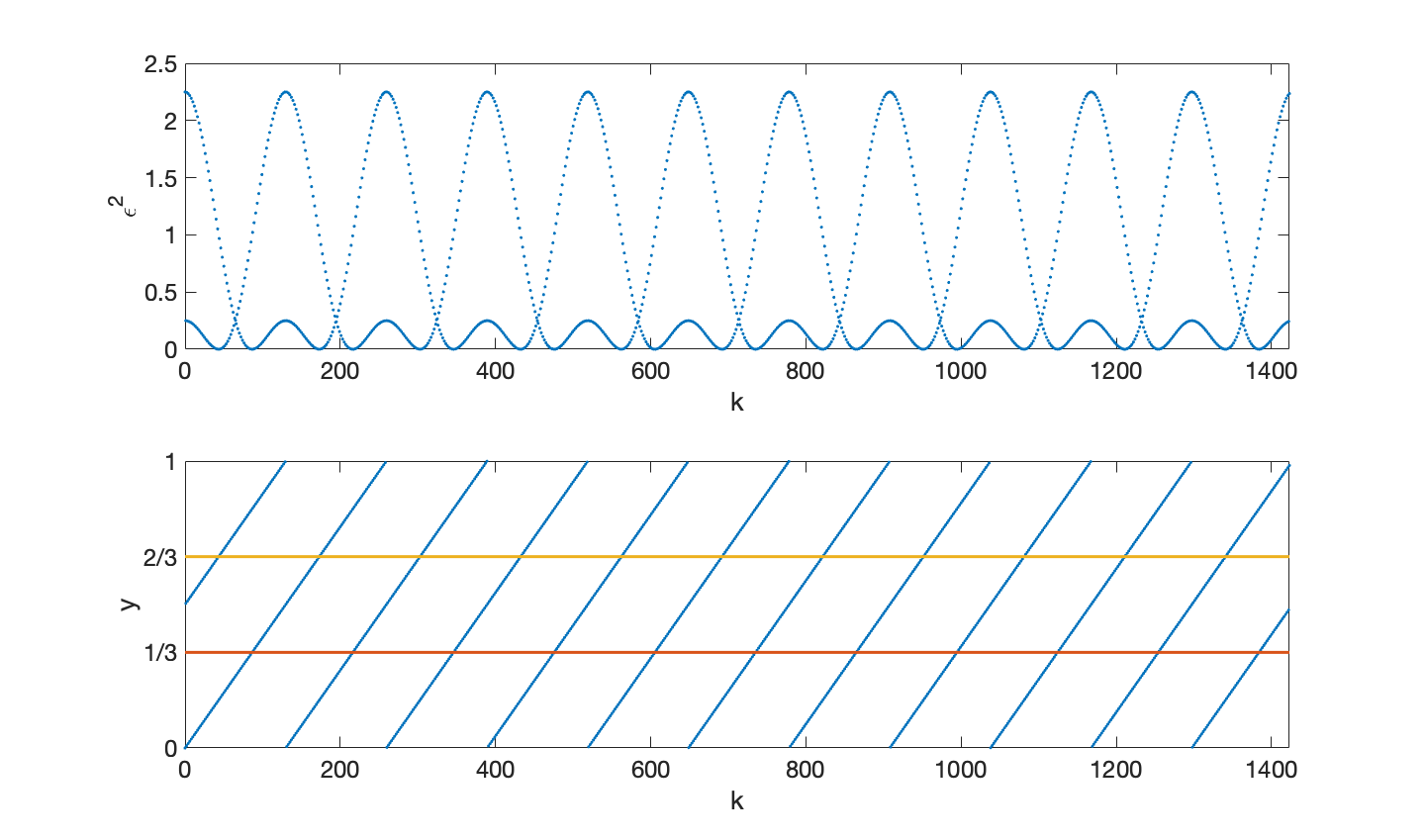
如果將時間離散化,最小單位取一秒,通過編程很容易找到最小的22個值的位置,和預測比較(單位為秒)
| 實際 | k值 | 預測 |
|---|---|---|
| 1302 | 43 | 1301.75 |
| 2604 | 86 | 2603.50 |
| 5207 | 172 | 5207.01 |
| 6569 | 217 | 6569.31 |
| 9173 | 303 | 9172.81 |
| 10475 | 346 | 10474.56 |
| 13078 | 432 | 13078.07 |
| 14380 | 475 | 14379.82 |
| 17044 | 563 | 17043.87 |
| 18346 | 606 | 18345.62 |
| 20949 | 692 | 20949.12 |
| 22251 | 735 | 22250.88 |
| 24854 | 821 | 24854.38 |
| 26156 | 864 | 26156.13 |
| 28820 | 952 | 28820.18 |
| 30012 | 995 | 30121.93 |
| 32725 | 1081 | 32725.44 |
| 34027 | 1124 | 34027.19 |
| 36631 | 1210 | 36630.69 |
| 37993 | 1255 | 37932.99 |
| 40596 | 1341 | 40596.50 |
| 41898 | 1384 | 41898.25 |
後記
後面的討論只是小擾動的近似,因為精確解是很難求出來的,而近似能夠足夠精準預測解的位置和大小。
22個點當中最小的是中間的兩個,$t = 20949$或$t = 22251$,分別對應十二小時中的5時49分9秒與6時10分51秒,這是考慮整數時間的情況,需要分別代入比較才能得到。但如果允許時間有小數,那麼由近似方法直接給出的$k$值分別為346和1081,對應時間為10474.56和32725.44,即2時54分34.56秒與9時5分25.44秒,精確為全局最小,可以通過程序很容易證明這一點。
補充
關於該時刻不存在有一個簡單的證明,假設時鐘走過的角度為$\theta$,那麼分鐘和秒針走過的角度就分別為$\theta\cdot\omega_2/\omega_3 = 12\theta$,$\theta\cdot\omega_1/\omega_3 = 720\theta$。因此
$$
708\theta \equiv 11\theta \equiv -719\theta \equiv \pm\frac{2\pi}{3} \mod 2\pi
$$
這是因為若秒針相對分針走過的角度為$\frac{2\pi}{3}$,分鐘相對時針走過的就不可能是$-\frac{2\pi}{3}$,否則秒針和時針就重疊了,後面同理。
這樣實際上要求
$$
697\theta \equiv 730\theta \equiv 0 \mod 2\pi
$$
然而$697\theta$和$730\theta$的最大公倍數只有$\theta$,這意味著
$$
\theta \equiv 0 \mod 2\pi
$$
然而這是不可能的,所以得證。
此外,關於全局最優解,可以找出相應的$k$值。這裡將問題一般化,即考慮
$$
y(k) = k\frac{m}{n} - \lfloor k\frac{m}{n}\rfloor,\ k = 0,2,…,n-1
$$
其中$m$和$n$是互質的兩個整數,$n > m$,何時最接近一個具體值$q$。可以令
$$
km = k’ + tn
$$
其中$t$要求滿足$km/n - 1 < t \leq km/n$且是一個整數,容易發現$t$可以從零取到$m-1$之間的任一自然數。這樣原問題即變為
$$
y(k’) = \frac{k’}{n}
$$
何時最接近$q$。考慮條件
$$
\left[y(k’) - q\right]^2 \leq \left[y(k’+1) - q\right]^2
$$
以及
$$
\left[y(k’) - q\right]^2 \leq \left[y(k’-1) - q\right]^2
$$
得到
$$
nq - \frac{1}{2} \leq k’ \leq nq + \frac{1}{2}
$$
在這個範圍內找到的整數解記作$k_c$,如果考慮只有一邊封閉的情況,這個解存在並且唯一。因此帶回得到
$$
k = \frac{k_c + tn}{m},\ t = 0,1,…,m-1
$$
並要求其為整數的情況。即
$$
k_c + tn \equiv 0 \mod m
$$
考慮$n$通常很大,假設
$$
n \equiv n’ \mod m
$$
也即要求
$$
k_c + tn’ \equiv 0 \mod m
$$
帶入具體例子,考慮$m = 719$,$n = 1427$,$q = 1/3$時,解出$k_c = 476$,可以取$n’ = -11$,則$t = 174$,解得$k = 346$。另一個$q = 2/3$時的解是對稱的,可以寫出來
$$
\begin{align}
& k_1 = \frac{k_{1c} + t_1n}{m}\\
& k_2 = \frac{k_{2c} + t_2n}{m}\\
& k_{1c} + t_1n \equiv 0 \mod m\\
& k_{2c} + t_2n \equiv 0 \mod m\\
& nq_1 - \frac{1}{2} \leq k_{1c} \leq nq_1 + \frac{1}{2}\\
& nq_2 - \frac{1}{2} \leq k_{2c} \leq nq_2 + \frac{1}{2}\\
\end{align}
$$
若$q_1 + q_2 = 1$,捨棄掉一些情況,容易解出$k_1 + k_2 = n$。
一個問題是$t$解一定是否存在,是一定的,可以簡單證明$m$除$k_c + tn$的餘數兩兩不等。假設存在$k_c + t_1n$與$k_c + t_2n$同餘,則
$$
(t_1 - t_2)n \equiv 0 \mod m
$$
考慮到$m$和$n$互質,則
$$
t_1 - t_2 \equiv 0 \mod m
$$
由於$t$是小於$m$的自然數,這種情況是沒有可能的。因此餘數兩兩不等,考慮$m$個$t$對應$m$個不同的餘數,則必然有一個餘數為零,即解存在並且唯一。