引言
這裡考慮液滴的形狀。
模型
在這之前需要計算極坐標系下切線的方向,用$\hat r$和$\hat \theta$表示徑向和切向的單位矢量。考慮$d\theta \to 0$時
$$
\begin{equation}
\begin{aligned}
\vec r(\theta + d\theta) - \vec r(\theta) =& r(\theta+d\theta)\hat r(\theta+d\theta) - r(\theta)\hat r(\theta)\\
\approx& [ r(\theta) + r’(\theta)d\theta ] [\hat r + d\theta\hat\theta] - r(\theta)\hat r\\
\approx& [ r’(\theta)\hat r + r(\theta)\hat \theta ]d\theta
\end{aligned}
\end{equation}
$$
將切線方向單位矢量記為$\hat\tau$(角度增加方向)
$$
\hat\tau = \frac{r’(\theta)\hat r + r(\theta)\hat \theta}{\sqrt{[r’(\theta)]^2 + r^2(\theta)}} = \frac{k(\theta)\hat r + \hat \theta}{\sqrt{k^2(\theta) + 1}}
$$
其中$k(\theta) = r’(\theta) / r(\theta)$。同樣的,法線方向單位矢量記為$\hat n$(向外方向)
$$
\hat n = \frac{\hat r - k(\theta)\hat \theta}{\sqrt{k^2(\theta) + 1}}
$$
表面張力
將極點固定在接觸面的中心,豎直方向為極軸,考慮任意一個液滴的截面,用$r$和$\theta$描述其與空氣的分界線。現在考察表面一小塊面元$r(\theta)d\theta dl$($dl$垂直于參考面),平衡時的受力為
$$
(p+p_0)r(\theta)d\theta dl \cdot \hat n + 2\gamma dl\cdot \left[ \hat\tau\left(\theta+\frac{d\theta}{2}\right) - \hat\tau\left(\theta-\frac{d\theta}{2}\right) \right] = \vec 0
$$
其中$\gamma$為水的表面張力,$p_0$為液體頂部與大氣壓強之差,注意$p_0$是未知的參數。由液體重力引起的壓強可以簡單給出
$$
p = \rho g [r(0) - r(\theta)\cos\theta]
$$
其中$\rho$為水的密度。現在估計切向單位矢量之差
$$
\begin{equation}
\begin{aligned}
\hat\tau\left(\theta+\frac{d\theta}{2}\right) - \hat\tau\left(\theta-\frac{d\theta}{2}\right) =& \frac{k\left(\theta+\frac{d\theta}{2}\right)\hat r\left(\theta+\frac{d\theta}{2}\right) + \hat \theta\left(\theta+\frac{d\theta}{2}\right)}{\sqrt{k^2\left(\theta+\frac{d\theta}{2}\right) + 1}}\\
& - \frac{k\left(\theta-\frac{d\theta}{2}\right)\hat r\left(\theta-\frac{d\theta}{2}\right) + \hat \theta\left(\theta-\frac{d\theta}{2}\right)}{\sqrt{k^2\left(\theta-\frac{d\theta}{2}\right) + 1}}\\
\approx& \left[k^2(\theta) + 1\right]^{-3/2}k’(\theta)\frac{d\theta}{2}\left[ \hat r\left(\theta+\frac{d\theta}{2}\right) + \hat r\left(\theta-\frac{d\theta}{2}\right) \right]\\
& - k\left[k^2(\theta) + 1\right]^{-3/2}k’(\theta)\frac{d\theta}{2}\left[ \hat\theta\left(\theta+\frac{d\theta}{2}\right) + \hat\theta\left(\theta-\frac{d\theta}{2}\right) \right]\\
& + k\left[k^2(\theta) + 1\right]^{-1/2}\left[ \hat r\left(\theta+\frac{d\theta}{2}\right) - \hat r\left(\theta-\frac{d\theta}{2}\right) \right]\\
& + \left[k^2(\theta) + 1\right]^{-1/2}\left[ \hat\theta\left(\theta+\frac{d\theta}{2}\right) - \hat\theta\left(\theta-\frac{d\theta}{2}\right) \right]\\
\approx& \left[k^2(\theta) + 1\right]^{-3/2}k’(\theta)d\theta\hat r - k\left[k^2(\theta) + 1\right]^{-3/2}k’(\theta)d\theta\hat\theta\\
& + k\left[k^2(\theta) + 1\right]^{-1/2}d\theta\hat\theta - \left[k^2(\theta) + 1\right]^{-1/2}d\theta\hat r\\
=& -\left[1 - \frac{k’(\theta)}{k^2(\theta) + 1} \right]d\theta\hat n
\end{aligned}
\end{equation}
$$
這裡近似考慮了一階展開。代回可以得到
$$
\rho g r(\theta)[r(0) - r(\theta)\cos\theta] + p_0r(\theta) = 2\gamma \left[1 - \frac{k’(\theta)}{k^2(\theta) + 1} \right]
$$
令$r_0 = r(0)$,$s = 2\gamma/(\rho g)$,以及$h = p_0/(\rho g)$,可以得到
$$
r(r_0 - r\cos\theta + h) = s\frac{r^2 + 2(r’)^2 - rr’’}{r^2 + (r’)^2}
$$
注意這裡把$r_0$看成一個常數,最後需要額外的自洽條件解出。結果如下圖所示,圖中重力的方向向左。
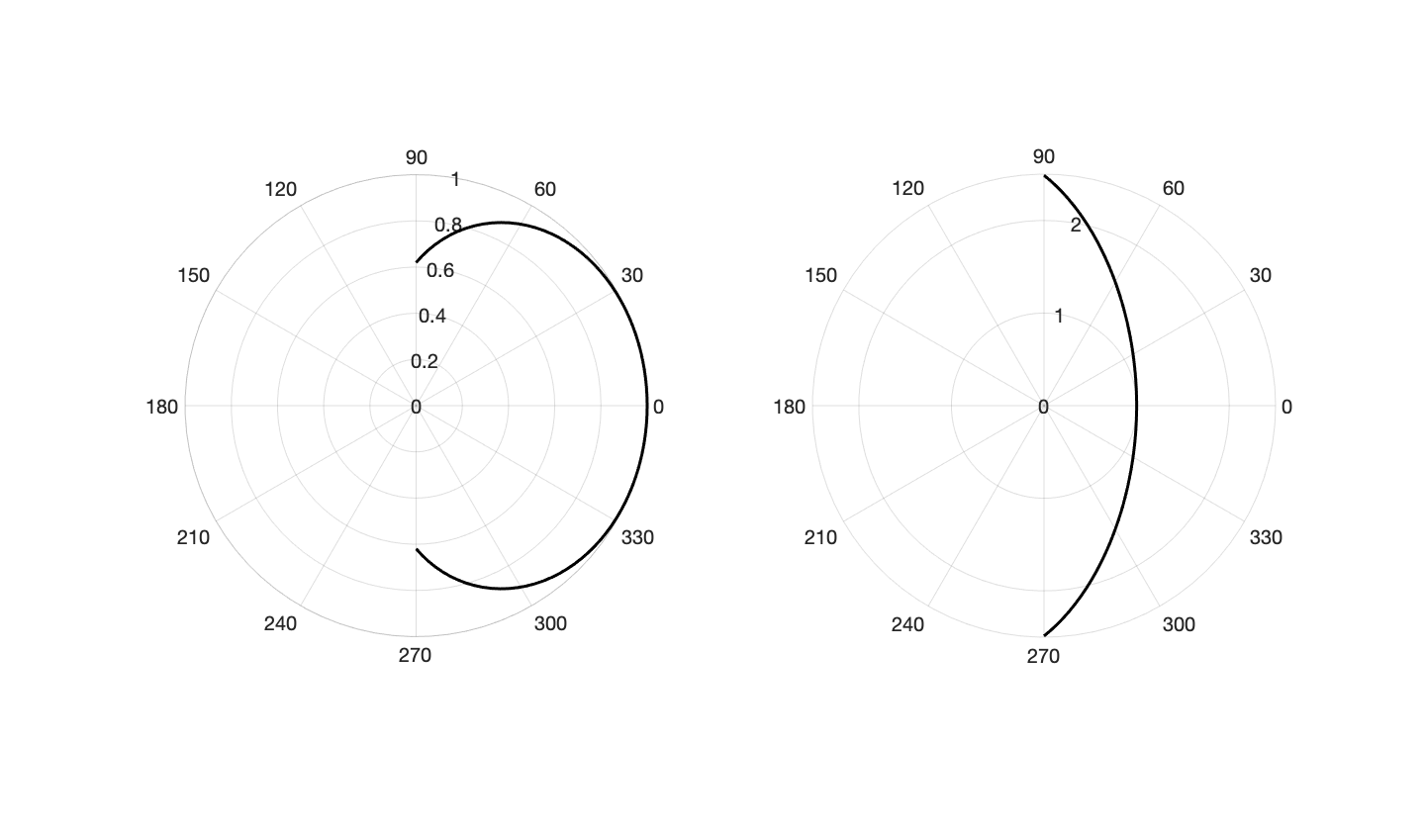
類似通過改寫壓強項,很容易得到液滴下垂的形狀,圖中重力方向向右
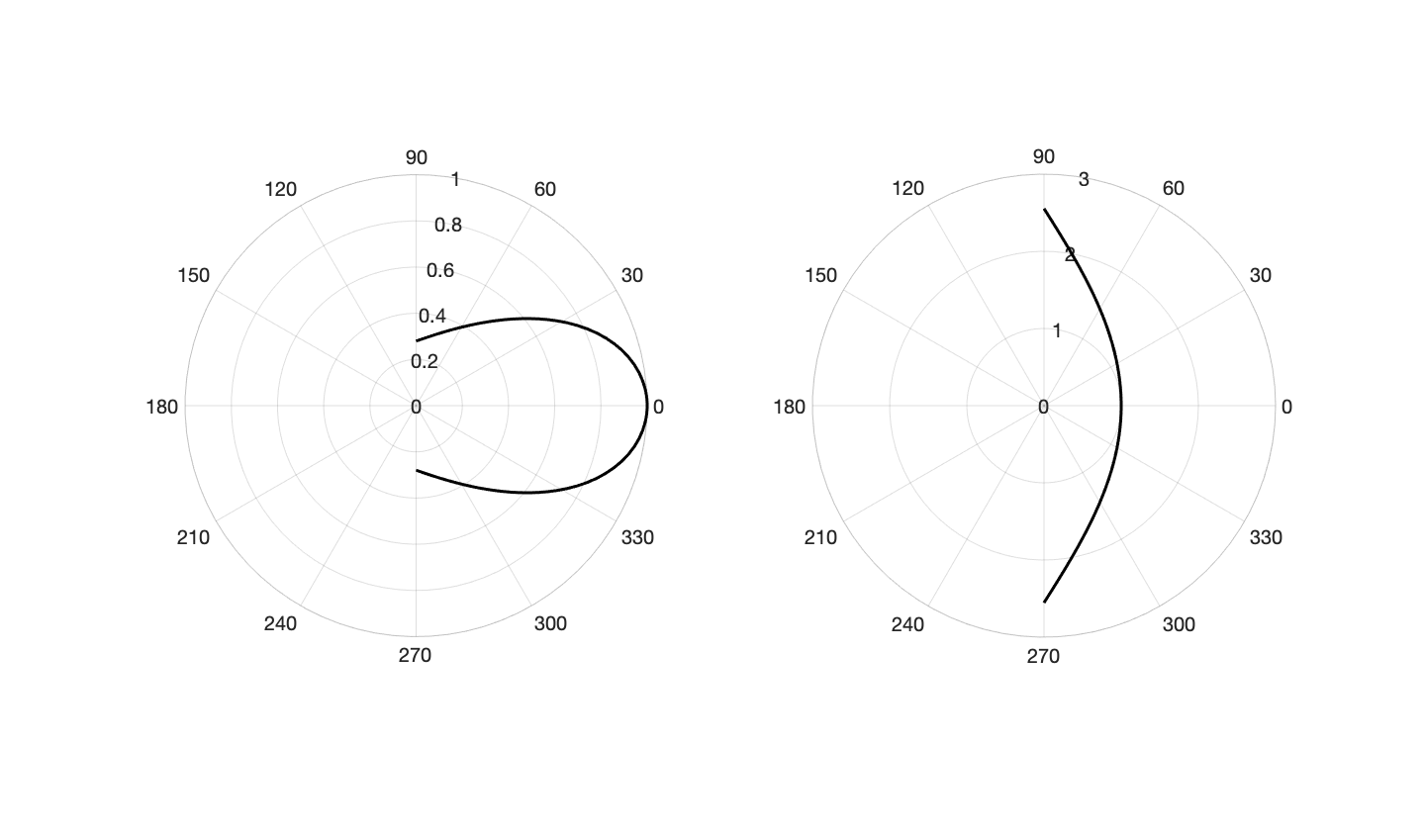
以及貼在垂直附著面上的形狀,圖中重力方向向下
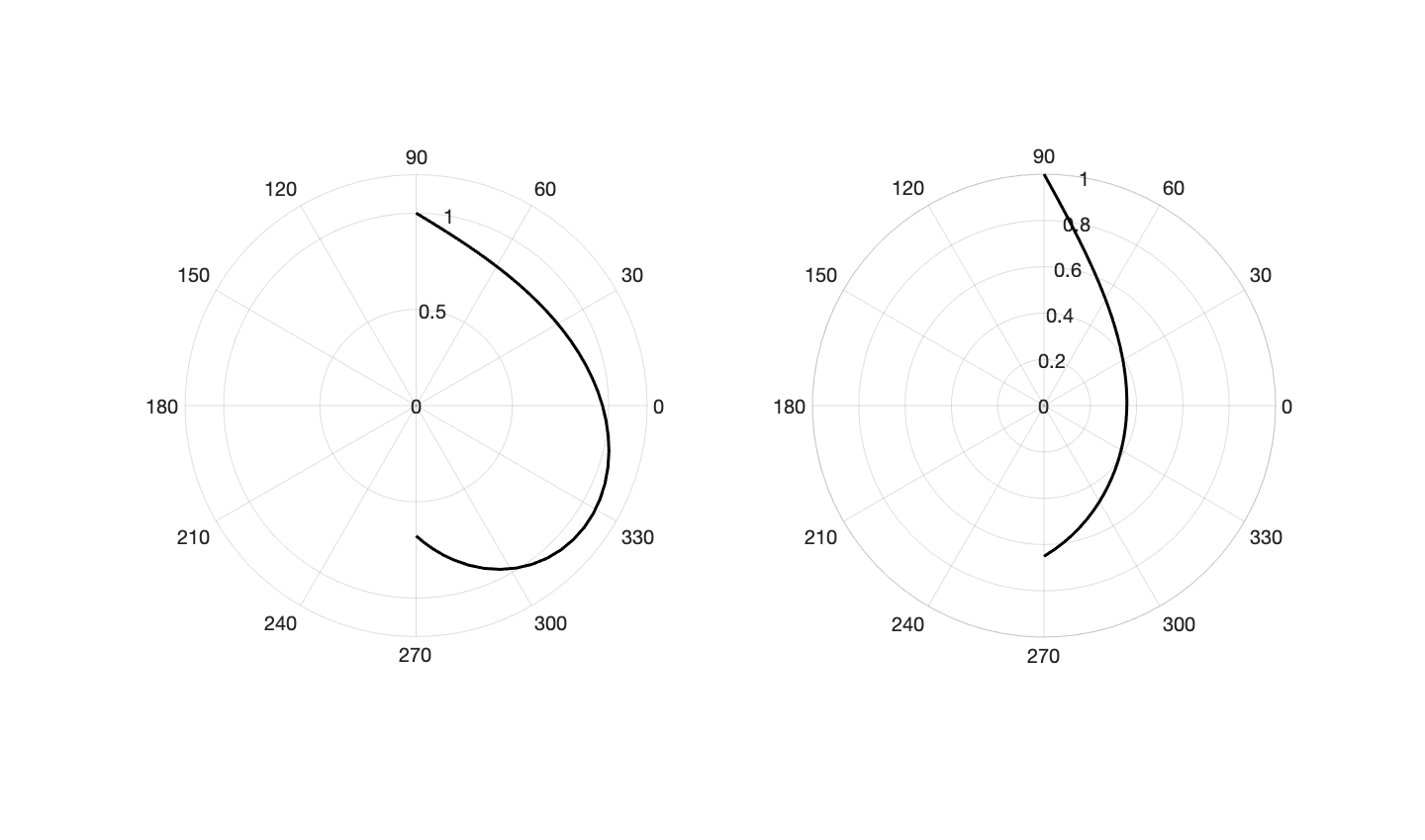
漸近行為
下面分析漸近行為,考慮$\theta \to 0$時,這時候方程退化為
$$
r^2 + 2(r’)^2 - rr’’ = \frac{h}{s}r\left[r^2 + (r’)^2\right]
$$
顯然$r(\theta) = r_0 = s/h$是方程的一個解,因此在角度很小的時候曲線是近圓的,即考慮近軸光線時可以將其作為一個完美的半球去處理,半徑即為液滴高度。
考慮$\theta \to \pi/2$時,這時候方程退化為
$$
r(r_0+h) = s\frac{r^2 + 2(r’)^2 - r_1r’’}{r^2 + (r’)^2}
$$
現在考慮右邊分子中的最後一項和前一項的量級比較
$$
\frac{rr’’}{(r’)^2} = \frac{r}{(r’)^2}\frac{dr’}{dr}\frac{dr}{d\theta} = r\frac{d\ln(r’)}{dr}
$$
假設$\ln(r’)$的按$dr$變化是個小量,略去$r’’$。因此方程簡化為
$$
\frac{dr}{d\theta} = \pm \sqrt{\frac{[r(r_0+h)-s]r^2}{2s-r(r_0+h)}}
$$
記$r_1 = r(\pi/2)$為接觸面半徑
$$
r’\left(\frac{\pi}{2}\right) = \pm \sqrt{\frac{[r_1(r_0+h)-s]r_1^2}{2s-r_1(r_0+h)}}
$$
令$\eta = \sqrt{[(r_0+h)r_1-s)/[2s-(r_0+h)r_1]}$。由此可以解出接觸角,其切線方向為
$$
\hat \tau_1 = \frac{k\left(\frac{\pi}{2}\right)\hat r + \hat \theta}{\sqrt{k^2\left(\frac{\pi}{2}\right) + 1}} = \frac{\pm\eta\hat r + \hat \theta}{\sqrt{\eta^2 + 1}}
$$
由以上正切值$\pm\eta$即可得到角度。
求解
注意到這個方程存在一個解$r(\theta) = (r_0+h)\sec\theta$,但這個解沒有意義,因為在$\theta = 0$處會導致矛盾的結果。
嘗試解這個非線性方程,先將方程寫成
$$
r[r_0 + h - r\cos\theta] = s\left[1 - \frac{k’}{k^2 + 1}\right]
$$
假設
$$
\frac{k’}{k^2 + 1} = c_1
$$
考慮$\theta$的對稱性,這個方程的解為$r(\theta) = c_2\sec(c_1\theta)$,代回原來方程得到
$$
c_2\sec(c_1\theta)\left[(r_0 + h) - c_2\sec(c_1\theta)\cos\theta\right] = s(1-c_1)
$$
當$\theta = 0$時,$r_0 = c_2$,因此
$$
r_0^2\sec(c_1\theta)\left[\left(1 + \frac{h}{r_0}\right) - \sec(c_1\theta)\cos\theta\right] = s(1-c_1)
$$
如果$\theta \to 0$,則
$$
c_1 \approx 1 - \frac{r_0h}{s}
$$
則方程的解近似為
$$
r(\theta) \approx r_0\sec\left[\left(1 - \frac{r_0h}{s}\right)\theta\right]
$$
這是非常粗糙的近似解。如果考慮$r_0 = s/h$,則$r(\theta) = r_0$,表明在近軸情況下是個球面。