引言
這裡計算一個特例,即$P = (I+H)(I+H)^T$的特徵值分佈,其中$H$是一個$N \times N$的隨機矩陣,每個元素$h_{ij}$均從均值為零,方差為$1/N$的正態分佈。
方法
首先注意到這個等式(對分塊矩陣取逆可得)
$$
\begin{equation}
\frac{1}{2N}\text{Tr}[zI - \tilde P]^{-1} \equiv
\frac{1}{2N}\text{Tr}
\begin{bmatrix}
zI & -(I+H) \\
-(I+H)^T & zI
\end{bmatrix}^{-1} = \frac{z}{N}\text{Tr}[z^2I - P]^{-1}
\end{equation}
$$
即Cauchy Transform有如下關係
$$
\tilde g(z) = zg(z^2)
$$
此外注意到
$$
\begin{equation}
\tilde P^2 =
\begin{bmatrix}
(I+H)(I+H)^T & 0 \\
0 & (I+H)^T(I+H)
\end{bmatrix} =
\begin{bmatrix}
P & 0 \\
0 & \mathcal{P}
\end{bmatrix}
\end{equation}
$$
這裡將其Cauchy Transform記作$\tilde g_2(z)$,注意到$P$與$\mathcal{P}$特徵值分佈完全相同,因此有
$$
g(z) = \tilde g_2(z)
$$
這樣問題就轉化為求$\tilde P^2$的Cauchy Transform。
自洽方程
由上述討論容易得到
$$
\tilde G(z) = z\tilde G_2(z^2)
$$
這裡記$G(z) = \langle zI-P \rangle$以及$\mathcal{G}(z) = \langle zI-\mathcal{P} \rangle$。因此
$$
\begin{equation}
\tilde G_2(z^2) =
\begin{bmatrix}
G(z^2) & 0 \\
0 & \mathcal{G}(z^2)
\end{bmatrix}
\end{equation}
$$
接下來尋找$\tilde G(z)$的一組自洽方程。注意到
$$
\begin{equation}
\tilde P =
\begin{bmatrix}
0 & I \\
I^T & 0
\end{bmatrix} +
\begin{bmatrix}
0 & H \\
H^T & 0
\end{bmatrix} = B + C
\end{equation}
$$
其中$C$是隨機矩陣而$B$給定。
根據Free Probability Theory
$$
\begin{equation}
\tilde G(z) = \left\langle \left[z - \eta(\tilde G) - B\right]^{-1} \right\rangle
\end{equation}
$$
其中$\eta(\tilde G) = \langle C\tilde GC \rangle$,這樣只需要將$\tilde G(z)$替換掉就可以得到關於$\tilde G_2(z^2)$的自洽方程組。
對這一條公式做一些解釋。這裡主要用到$B$和$C$相互自由,因而其和的R Transform將等於分項之和,這樣做的好處是可以把$B$分離出來,也被稱為subordination property,即
$$
G_{x+y}(z) = G_x[z - R_y(G(z))]
$$
其中
$$
R_{x+y}(z) = R_x(z) + R_y(z)
$$
由此可以推出
$$
\tilde G(z) = G_B[z-R_C(\tilde G)] = \left\langle \left[z - \eta(\tilde G) - B\right]^{-1} \right\rangle
$$
如果類比費曼圖,R Transform相當於self energy。 此外由於$C$是operator-valued semi-circular element,$\tilde G(z)$的R Transform將等於$\eta(\tilde G)$。
計算
首先計算
$$
\begin{equation}
\eta(\tilde G) = \eta[z\tilde G_2(z^2)] = z\left\langle C\tilde G_2(z^2)C \right\rangle = z\left\langle \begin{bmatrix}
H\mathcal{G}(z^2)H^T & 0 \\
0 & H^TG(z^2)H
\end{bmatrix}
\right\rangle
\end{equation}
$$
因此
$$
\begin{equation}
\tilde G(z) = \left\langle
\begin{bmatrix}
z - z\langle H\mathcal{G}(z^2)H^T \rangle & -I \\
-I & z - z\langle H^TG(z^2)H\rangle
\end{bmatrix}^{-1}
\right\rangle、
\end{equation}
$$
根據Schur complement formula
$$
\begin{equation}
\begin{bmatrix}
A & B \\
C & D
\end{bmatrix}^{-1}
=
\begin{bmatrix}
\left(A-BD^{-1}C\right)^{-1} & -A^{-1}B\left(D-CA^{-1}B\right)^{-1} \\
-D^{-1}C\left(A-BD^{-1}C\right)^{-1} & \left(D-CA^{-1}B\right)^{-1}
\end{bmatrix}
\end{equation}
$$
藉此可以寫出方程
$$
\begin{equation}
zG(z^2) = \left\langle \left[ z - z\langle H\mathcal{G}(z^2)H^T \rangle - \frac{1}{z - z\langle H^TG(z^2)H\rangle} \right]^{-1} \right\rangle
\end{equation}
$$
整理得到
$$
zg(z) = \left[ 1 - g(z) - \frac{1}{z-zg(z)} \right]^{-1}
$$
即
$$
z = \frac{1}{g(z)[1-g(z)]^2}
$$
最後通過Stieltjes Transform可以得到特徵值分佈
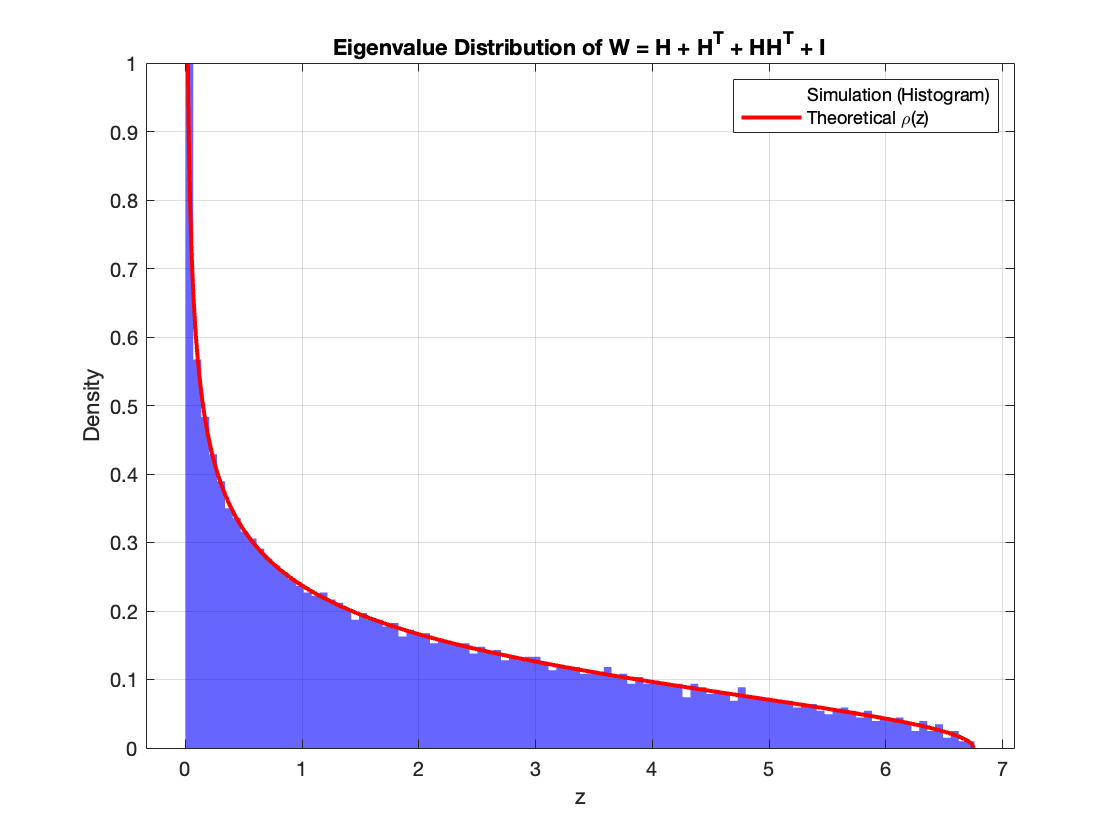
後記
我傾向認為不能用Cavity Method直接處理此類問題,也許其變種可以。無論如何這是我能找到的處理此類問題最簡單的辦法了。